ネットワークのことでちょっとした疑問があるので実験しようと思っていたんだけど、そういや生成AIという手段があったことを思い出したのでまずは聞いてみることにした。
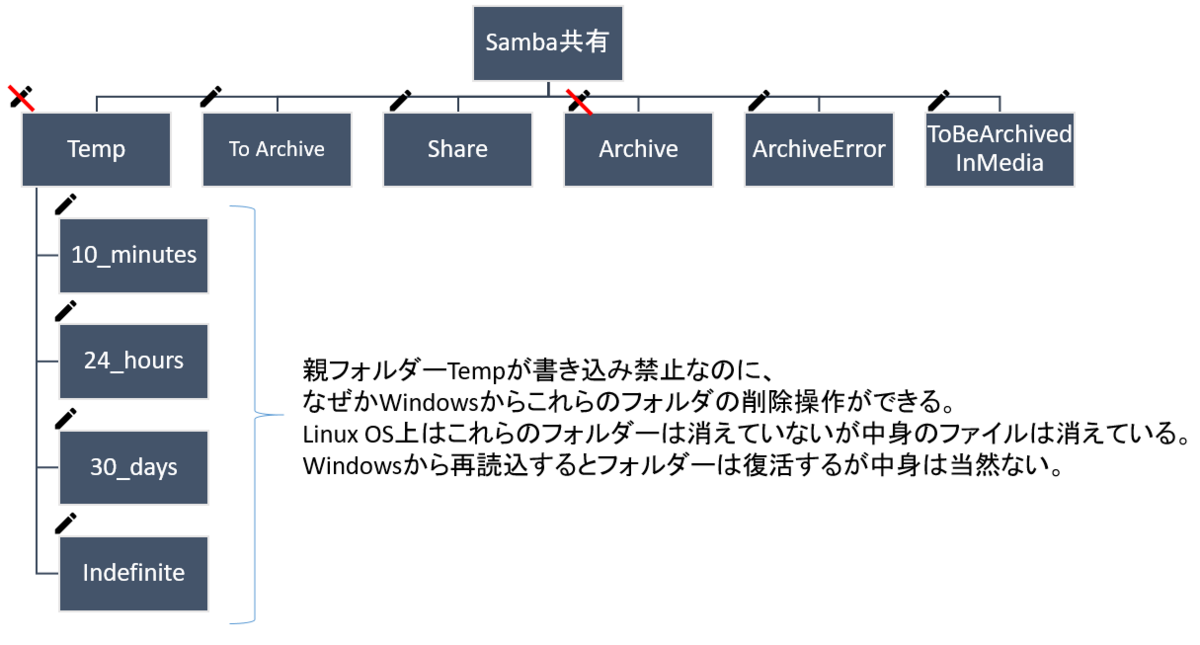
何かというと、VLANをサポートしていないアンマネージドスイッチをマネージドスイッチのVLANポートに繋いだとき、そのクライアントが正しくVLANに所属できるのかどうかということ。
図示するとこんな感じ。

このときPC1はPC2とは当然繋がり、PC3ともVLAN経由で繋がり、PC4は別VLANだから繋がらないという動作になれば想定どおり。
今回使ったのはGoogle Gemini。
結構長くなるので先に結論を書くと、誤りも多く鵜呑みにはできないものの仕組みの理解や追加の理解のためのヒントとして仮説を立てるのには非常に有益だった。
具体的な質問と回答はこんな感じになった。
Q:スマートスイッチのポートVLANがアサインされたポートにアンマネージドスイッチを接続した場合、そのアンマネージドスイッチに接続したクライアントはそのVLANに所属しますか。
A:はい、そのアンマネージドスイッチに接続したクライアントは、スマートスイッチのポートVLANに所属します。
理由:
スマートスイッチのポートVLANは、802.1Qトランキングを使用して、アンマネージドスイッチに伝達されます。
802.1Qトランキングは、VLAN情報をパケットヘッダーに含めるため、アンマネージドスイッチは、接続されているポートのVLAN情報を認識できます。
アンマネージドスイッチは、VLAN情報に基づいて、パケットを適切なポートに転送します。ただし、以下の点に注意が必要です:
アンマネージドスイッチは、VLAN設定を認識できないため、VLAN間ルーティングはできません。
アンマネージドスイッチに接続されたクライアントは、同じVLAN内の他のクライアントとしか通信できません。
異なるVLAN間の通信には、ルーターが必要です。
続けて聞いてみた。間違えてトラッキングって書いてしまったけど意図を理解して回答してくれた。
Q:802.1Qトラッキングはアンマネージドスイッチでもサポートされているのですか。
A:はい、802.1Qトランキングはアンマネージドスイッチでも一部サポートされています。
アンマネージドスイッチにおける802.1Qトランキングのサポート状況:
トランキングのネゴシエーション:
多くのアンマネージドスイッチは、トランキングのネゴシエーションをサポートしていません。
そのため、トランキングを有効にするには、スマートスイッチ側でポート設定を手動で設定する必要があります。
VLAN情報の認識:
アンマネージドスイッチは、VLAN情報を認識できます。
ただし、VLAN間ルーティングはできません。
VLANごとのポート設定:
アンマネージドスイッチは、VLANごとのポート設定をサポートしていない場合があります。
すべてのポートが同じVLANに属するデフォルト設定のみの場合があります。アンマネージドスイッチで802.1Qトランキングを使用する場合の注意点:
トランキングのネゴシエーションをサポートしていない場合は、スマートスイッチ側でポート設定を手動で設定する必要があります。
VLAN間ルーティングはできません。
VLANごとのポート設定をサポートしていない場合は、すべてのポートが同じVLANに属します。
トランキングの意味が分かってなかったので更に聞いてみた。
Q:トランキングとは何のことですか。また英語でのスペルを教えてください。
A:トランキングとは、複数の物理的な通信回線や周波数チャネルを束ねて、1つの論理的な回線として扱う技術です。これにより、以下のメリットを得ることができます。
回線の効率的な利用: 複数の回線を束ねることで、全体的な通信容量を増加させることができます。
冗長性の向上: 1つの回線が故障しても、他の回線で通信を継続することができます。
拡張性の向上: 必要に応じて、簡単に回線を追加することができます。トランキングは、さまざまな分野で利用されています。
電話ネットワーク: 電話交換機間を接続する回線にトランキングがよく使われます。
データ通信ネットワーク: ルーター間を接続する回線や、サーバー間の接続にもトランキングが使われます。
無線LAN: 複数のアクセスポイントをまとめて管理するためにトランキングが使われます。トランキングの英語
トランキングの英語は**「trunking」**です。
**「trunk」**は、「木の幹」や「荷物入れ」という意味の単語です。
トランキングは、複数の回線を束ねて1つの大きな回線にすることから、この単語が使われています。トランキングの種類
トランキングには、いくつかの種類があります。
リンクトランキング: 複数の物理的な回線を束ねて、1つの論理的な回線として扱う方式です。
チャネルトランキング: 1つの物理的な回線を複数の論理的なチャネルに分割して、それぞれ独立した通信路として扱う方式です。
ポートトランキング: 複数のスイッチポートを束ねて、1つの論理的なポートとして扱う方式です。トランキングのまとめ
トランキングは、複数の回線を束ねて1つの論理的な回線として扱う技術です。これにより、回線の効率的な利用、冗長性の向上、拡張性の向上などのメリットを得ることができます。
トランキングには、リンクトランキング、チャネルトランキング、ポートトランキングなど、いくつかの種類があります。
参考情報トランキング - Wikipedia: https://es.wikipedia.org/wiki/Ranking
Trunking - Techopedia: https://www.crunchbase.com/organization/techopedia
なんでも教えてくれる。
しかしアンマネージドスイッチが802.1Qトランキングなんていう専門的な機能をサポートしているなんていう話は聞いたことが無かった。内部動作としてそうなっているっていうことなんだろうけど所詮Ciscoとかの業務用アンマネージドスイッチだけなのでは?と疑って続けて聞いてみた。
Q:エレコムのアンマネージドスイッチは802.1Qトランキングをサポートしていますか
A:はい、エレコムのアンマネージドスイッチの一部は802.1Qトランキングをサポートしています。
エレコムのアンマネージドスイッチで802.1Qトランキングをサポートしているモデル:
LSW-TXシリーズ: 10GbE対応モデル
LSW-GTシリーズ: ギガビット対応モデル
LSW-GSシリーズ: 100BASE-TX対応モデルただし、以下の点に注意が必要です:
すべてのモデルがトランキングのネゴシエーションをサポートしているわけではありません。
VLANごとのポート設定をサポートしていないモデルもあります。詳細については、各製品のマニュアルを参照してください。
エレコムのアンマネージドスイッチで802.1Qトランキングを使用する例:
LSW-TXシリーズのスイッチのポート1をVLAN 10に設定し、アンマネージドスイッチのポート1に接続します。
アンマネージドスイッチのポート1は、VLAN 10に属するすべてのクライアントと通信できます。
VLAN 10以外のVLANに属するクライアントとは通信できません。代替案:
VLAN間ルーティングが必要な場合は、マネージドスイッチを使用する必要があります。
マネージドスイッチは、VLAN設定を詳細に設定できるため、より柔軟なネットワーク構成が可能です。参考情報:
エレコム公式サイト: https://www.elecom.co.jp/
LSW-TXシリーズ: [無効な URL を削除しました]
LSW-GTシリーズ: [無効な URL を削除しました]
LSW-GSシリーズ: [無効な URL を削除しました]
Q:トランキングのネゴシエーションをサポートしていないというのはトランキングをサポートしていないということとは別ですか?ネゴシエーションをサポートしていないにもかかわらずトランキングをサポートしているとはどういう状態を指しますか。
A:はい、トランキングのネゴシエーションをサポートしていないというのは、トランキングをサポートしていないとは別のことです。
トランキングのネゴシエーションとは、スイッチ間でトランキングの設定を自動的に設定するための仕組みです。この仕組みがサポートされていない場合、手動でトランキングの設定を行う必要があります。
トランキングをサポートしているとは、スイッチが複数の物理的な回線を束ねて1つの論理的な回線として扱う機能を持っていることを指します。
トランキングのネゴシエーションをサポートしていないにもかかわらずトランキングをサポートしている状態とは、以下の状態を指します。
スイッチは、複数の物理的な回線を束ねて1つの論理的な回線として扱う機能を持っている。
スイッチは、トランキングの設定を自動的に設定するための仕組みを持っていない。
トランキングを使用するには、スイッチの設定画面で手動でトランキングの設定を行う必要がある。例:
エレコムのアンマネージドスイッチ LSW-GS1016Tは、トランキングのネゴシエーションをサポートしていない。
LSW-GS1016Tは、トランキングをサポートしている。
LSW-GS1016Tでトランキングを使用するには、スイッチの設定画面で手動でトランキングの設定を行う必要がある。トランキングのネゴシエーションをサポートしていないスイッチでトランキングを使用する場合の手順:
スイッチの設定画面を開きます。
トランキングの設定画面に移動します。
トランキングを使用するポートを選択します。
トランキングのパラメータを設定します。
設定を保存します。参考情報:
トランキング - Wikipedia: [無効な URL を削除しました])
802.1Qトランキング - Techopedia: [無効な URL を削除しました]
こうなってくると逆にトランキングをサポートしていないスイッチがあるのか気になる。
Q:トランキングをサポートしていないスイッチはありますか。具体的な製品名も分かれば教えてください。
A:はい、トランキングをサポートしていないスイッチは存在します。いくつかの例を挙げます。
1. 古いスイッチ
古いスイッチは、トランキング機能が搭載されていない場合があります。具体的には、10年以上前に製造されたスイッチは、トランキングに対応していない可能性が高いです。
例:
Cisco Catalyst 2950シリーズ
3Com SuperStack 3 Switch 3300
Netgear ProSafe GS724T2. 低価格帯のスイッチ
低価格帯のスイッチは、コスト削減のため、トランキング機能が省略されている場合があります。
例:
TP-Link TL-SG105E
Buffalo LSW3-GT-8E
D-Link DGS-1008D3. 特殊な用途向けのスイッチ
特殊な用途向けのスイッチは、トランキング機能が必要ない場合があり、搭載されていないことがあります。
例:
PoEスイッチ
ファイバースイッチ
KVMスイッチ4. アンマネージドスイッチ
アンマネージドスイッチは、基本的にトランキング機能をサポートしていません。
例:
エレコム LSW-GS1016T
I-O DATA WN-GS1016T
BUFFALO LSW3-GT-8Eトランキングのサポート状況を確認する方法:
スイッチの製品マニュアルを確認する
スイッチのメーカーのWebサイトを確認する
スイッチの設定画面を確認するトランキングが必要かどうか:
トランキングが必要かどうかは、ネットワークの規模や構成によって異なります。以下の場合、トランキングが必要になる可能性があります。
複数のVLANを使用している
冗長性を向上させたい
ネットワークの帯域幅を増やしたいトランキングが必要な場合は、トランキング機能をサポートしているスイッチを選択する必要があります。
参考情報:
トランキング - Wikipedia: [無効な URL を削除しました])
802.1Qトランキング - Techopedia: [無効な URL を削除しました]
回答に矛盾を感じたので追加で確認。
Q:アンマネージドスイッチは、基本的にトランキング機能をサポートしていないという回答と、スマートスイッチのポートVLANが802.1Qトランキングを使用してアンマネージドスイッチに伝達されるという話は矛盾しませんか?
A:いいえ、矛盾しません。アンマネージドスイッチはトランキングの設定や管理機能をサポートしていないため、トランキングを直接設定することはできません。
しかし、802.1Qトランキングは、スイッチ間のVLAN情報の伝達にも使用されます。スマートスイッチは、アンマネージドスイッチに接続するポートにVLAN情報を802.1Qトランキングヘッダーに含めて送信します。アンマネージドスイッチは、この情報に基づいて、受信したパケットを適切なポートに転送します。
つまり、アンマネージドスイッチはトランキングの設定や管理はできないものの、802.1Qトランキングヘッダーを理解してVLAN情報の伝達には対応できます。
例:
スマートスイッチのポート1をVLAN 10に設定し、アンマネージドスイッチのポート1に接続します。
スマートスイッチからアンマネージドスイッチに送信されるパケットには、VLAN 10の情報が802.1Qトランキングヘッダーに含まれます。
アンマネージドスイッチは、この情報に基づいて、VLAN 10のポート1にパケットを転送します。注意点:
アンマネージドスイッチは、VLAN間ルーティングはできません。
異なるVLAN間の通信には、ルーターが必要です。参考情報:
802.1Qトランキング - Wikipedia: [無効な URL を削除しました])
VLAN - Wikipedia: [無効な URL を削除しました])
Q:ということは、先ほどトランキングをサポートしていないアンマネージドスイッチとして例示いただいたエレコムのLSW-GS1016Tでも、マネージドスイッチのポートVLANに接続すれば、そのクライアントはポートVLANに所属するということですね。
A:はい、その通りです。エレコムのLSW-GS1016Tのようなトランキング機能をサポートしていないアンマネージドスイッチであっても、マネージドスイッチのポートVLANに接続すれば、そのクライアントはポートVLANに所属します。
動作の詳細:
マネージドスイッチのポート1をVLAN 10に設定し、アンマネージドスイッチLSW-GS1016Tのポート1に接続します。
マネージドスイッチからLSW-GS1016Tに送信されるパケットには、VLAN 10の情報が802.1Qトランキングヘッダーに含まれます。
LSW-GS1016Tは、VLAN 10の情報に基づいて、ポート1に接続されたクライアントにパケットを転送します。
LSW-GS1016Tに接続されたクライアントは、VLAN 10に所属していることになります。注意点:
LSW-GS1016Tは、VLAN間ルーティングはできません。
異なるVLAN間の通信には、ルーターが必要です。補足:
LSW-GS1016Tのようなアンマネージドスイッチは、トランキングの設定や管理機能をサポートしていないため、ポートVLANの設定はできません。
ポートVLANの設定は、接続先のマネージドスイッチで行う必要があります。参考情報:
802.1Qトランキング - Wikipedia: [無効な URL を削除しました]
VLAN - Wikipedia: [無効な URL を削除しました]
これで概ね話は理解できた。
あとはこの回答にどれくらい信ぴょう性があるのかということだけど、実はエレコム製と紹介いただいたLSW-TXシリーズをGoogleで検索してみるとバッファロー製品であることがわかる。
さっそくツッコミをいれてみた。
Q:エレコムのスイッチとして紹介いただいたLSW-TXシリーズですが、Google検索するとバファロー製品がヒットします。本当にエレコム製品ですか?その場合は根拠となるリンクを教えてください。
A:ご指摘ありがとうございます。エレコムのスイッチとして紹介させていただいたLSW-TXシリーズは、誤りでした。LSW-TXシリーズはバッファロー製品です。
誤情報の原因:
情報収集時に、類似製品名の混同があった可能性があります。
情報源の信頼性確認が不十分でした。訂正:
エレコムのスイッチとして紹介したLSW-TXシリーズは、バッファロー製品です。
エレコムのトランキング対応アンマネージドスイッチの例としては、LSW-GS1016Tなどが挙げられます。根拠となるリンク:
バッファロー LSW-TXシリーズ: https://www.buffalo.jp/product/detail/lsw3-tx-8ns_wh.html
エレコム LSW-GS1016T: https://www.circulationheaters.org/circulation_heaters/MFLC1236X1026T.htmlお詫び:
誤った情報を提供してしまい、大変申し訳ございませんでした。今後は情報収集と情報源の信頼性確認を徹底し、このような誤情報の提供がないよう努めてまいります。
その他:
ご質問やご不明な点があれば、お気軽にご連絡ください。
さらにこの回答にあるLSW-GS1016TはGoogle検索でヒットせず、指定されたリンクはサーキュレーションヒーター(回転型ヒーター)。。
こうなってくると回答全体の信憑性もちょっと怪しい。
ただ考え方のヒントや検索する際のキーワードは手に入ったのであとは自分で調べてみることにした。
Redditの英語トピックでアンマネージドスイッチにおけるVLANパケットがどう扱われるのか興味深い説明が見つかった。
https://www.reddit.com/r/homelab/comments/1053p17/vlans_through_unmanaged_switch/
Depends on the switch. It could do any of the following:
Ignore packets with tagged VLAN
Only pass packets with no tag
Pass everything
Pass everything, rewriting the VLAN tag to 1
Drop everything
これを読むとやはりGemini AIが示した以下の回答は怪しくなってくる。
スマートスイッチは、アンマネージドスイッチに接続するポートにVLAN情報を802.1Qトランキングヘッダーに含めて送信します。アンマネージドスイッチは、この情報に基づいて、受信したパケットを適切なポートに転送します。
つまり、アンマネージドスイッチはトランキングの設定や管理はできないものの、802.1Qトランキングヘッダーを理解してVLAN情報の伝達には対応できます。
多くのスイッチが802.1Qトランキングヘッダーを理解してVLAN情報の伝達なんていう高度な事をやっているとは思えないのだ。
やはりAIの回答を鵜呑みにするというのはそれなりに危険だけど、何もヒントがないなかで色々と仮説を立ててその後の調査のヒントとするという使い方であればかなり役に立ちそうだと思った。