前回desmosという数学ソフトのサンプルとしてテイラー展開を示したが、私にはよく分からないと書いた。

ただこれ、よく思い出してみると三角関数のsin()の実装がどうなっているのか気になって最近調べたサイトで見かけたことがある。
hackemdown.blogspot.com
つまり以下の式を使えばsin関数を自分で作ることができるということらしい。
※少し話が脱線するが、はてなブログはTeX記法が使えるので上記の数式は以下のように書ける。
[tex: \displaystyle \sum_{n=0}^{a} \frac{ (-1)^{n}x^{2n+1}} {(2n+1)!}]少し複雑だけど有志がチートシートを公開しているのではてなブログで数式を書きたい時はTeX(てふ)について調べてみると良いかと思う。
…話をもどして、そのときはVBAでやろうとして階乗ですぐオーバーフローになったり、どこかで式の理解を間違えたのか値がズレすぎて諦めていた。
今回はSympyを使ってリベンジしてみる。
コードは以下の通り。
# 準備 import math from sympy import init_printing, symbols, Sum, factorial, summation, solve from sympy.plotting import plot %matplotlib inline init_printing(use_latex='mathjax') x,a,n = symbols('x a n') # 式の組立 y = Sum((-1)**n*x**(2*n+1)/factorial(2*n+1), (n, 0, a)) # 繰り返し回数 a の決定とプロット f = y.subs({a:20}) plot(f)
Google Colaboratory でやってみると次の通り。

おお、サイン波っぽいのでた!
できてるようだ。
しかし実際にxを代入して計算させたいけどうまくいかなかった。
次のように文字式のまま表示されてしまい、solveしても結果が現れない。

なんかやりようはあるんだろうけど一旦断念してSum()の代わりにsummation()という関数を使うことにする。
関数f2として作成するコードがこちら。
f2 = summation((-1)**n*x**(2*n+1)/factorial(2*n+1),(n,0,20))
Sumを使ったときと式は大体同じだが、繰り返し回数を表す文字aは消えている。
最後の(n,0,20)がその代わりとなるもので、nは0から20まで繰り返すという意味。
こうするとシグマではなくそのまま総和が展開された形の関数ができあがるようだ。

なんかすごいのが出てきてしまったが、plotするとやはりサイン波がでてる。
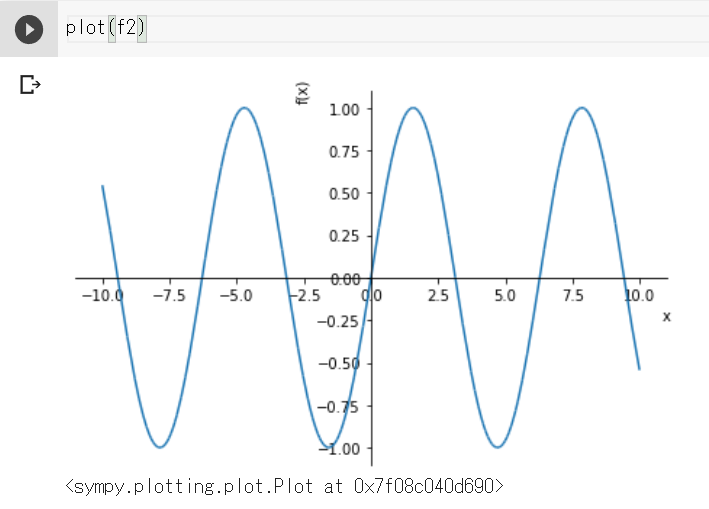
この関数f2(x)が本当にsinになっているのか、以下のとおりmath.sin()と比較してみた。
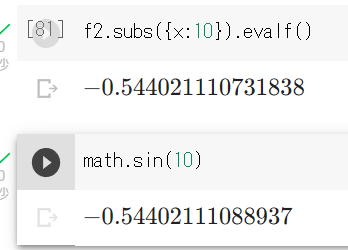
小数点以下9桁まで一致しているので、そこそこ精度は出ている。
繰り返し回数をもっと増やせば精度を高めることができるだろう。
以上。
。。。やるか。

ばーん!

うぉぉぉぉ!!!

オォォォォヲォォォ!

よし、完全一致。

数式でるまで30秒かかったのでまったく実用的ではないけども高精度sinが出来た。
真面目な話、繰り返し回数を増やしても浮動小数点型で表せる小数点以下の桁数に限界があるのでどこで打ち切るかが問題となる。
またSin(10)程度ならテイラー展開が精度も高くて現実的なスピードで計算できるけど、角度が増えると計算量が増えるので、C言語のライブラリでは一定角度以上はあらかじめ計算した値をライブラリ内で持っていてそれを返すという実装になってるらしい。
コード読んだわけじゃないので本当のことは知らないけど。
以上。