今読んでいる「マンガで分かる材料力学」で昨晩から格闘していた箇所がようやく理解できた。今回、私が記事に残しておきたかったのは問題の答えではなく、「分からない」から「分かった」へ移行する際の思考の道筋である。
端的に問題と解説だけ掲載しても他の問題に応用できることって限られているので、それほど価値があることとは思えない。それよりも、何かまた自分が壁にぶち当たった際に考え方のヒントになるような記事にしたいと思った。
分からなかったのは以下の赤枠で囲った一文。

ちなみに設問ですらなく、さも当然かのように書かれている。
しかしなぜそうなるのか分からない。いくら考えても分からない。
ここで一度立ち止まって原因を考えてみた。
なんで分からないのか?何を知らないから分からないのか?自問してみると答えは見つかった。
「そもそも楕円の面積の求め方しらねぇ。。」
そしてググると、次のような形で求められるらしい。
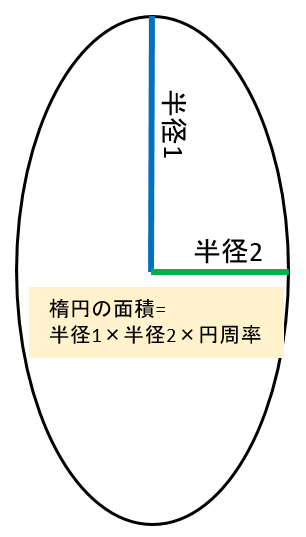
なるほど、楕円も正円を包含するので公式がそのまま当てはまる。
次にFusion 360でモデリングして考えてみた。
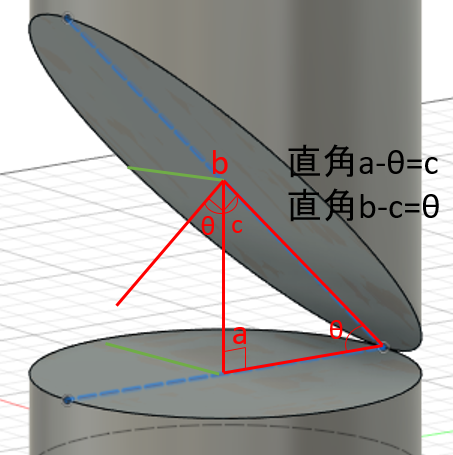
これはなかなか良いヒントを与えてくれたが、もっともらしく式を書いてみたものの合ってる確証が持てない。
まだまだ腑に落ちるというところまでは遠い。
次に平面で考えてみたが全然うまくいかない。
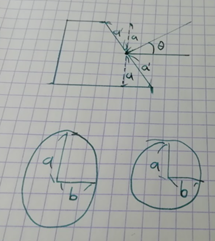
描いてる途中でモヤっとしてくる。
この「モヤっ」となる原因を冷静に考えてみたところ、角度・長さを示す記号や文字がどこを指しているいるのか途中で混乱していることに気づいた。正確にいうともっと印をつけたいけどこれ以上書くと判別できなくなるため無意識にブレーキをかけていた。
つまり、図が小さすぎて十分なスペースが確保できていないのだ。
更に、記号の使い分けも洗練されていないことに気づいた。例えば角度を表す記号をシータしか知らないため表現力に乏しい。
さらにググって「ファイ(φ)」という記号があることを知り、使ってみることにした。
極端に大きく書いてみたところ、かなり理解が進んだ。
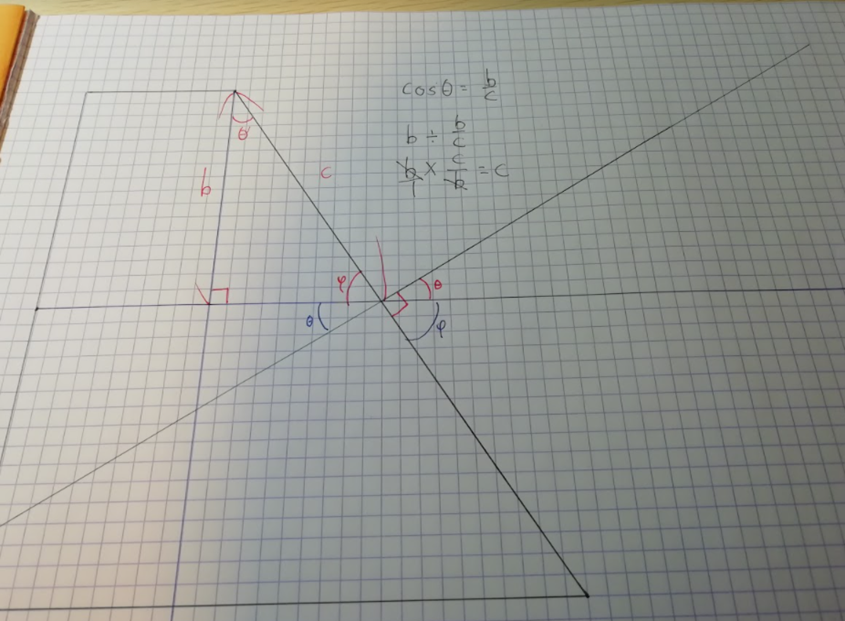
一見些細なようでいて、実は結構思考の妨げになっているということがある。
たとえばプログラミングでも、初心者はインデントが分からなかったり変数の名前付けが適当だったりする。それでもロジックが正しければプログラムは動くので些細な事だと思いがちなんだけど、難しい問題にぶち当たったときに実はインデントの乱れや適当な変数名が思考にモヤをかけていたなんてことは良くある。
クリアな思考を保つためにはやはり情報の表現力を磨いていく必要があるなと思った。
さて、次がn度目の正直。ようやくスッキリ理解できたときのメモである。
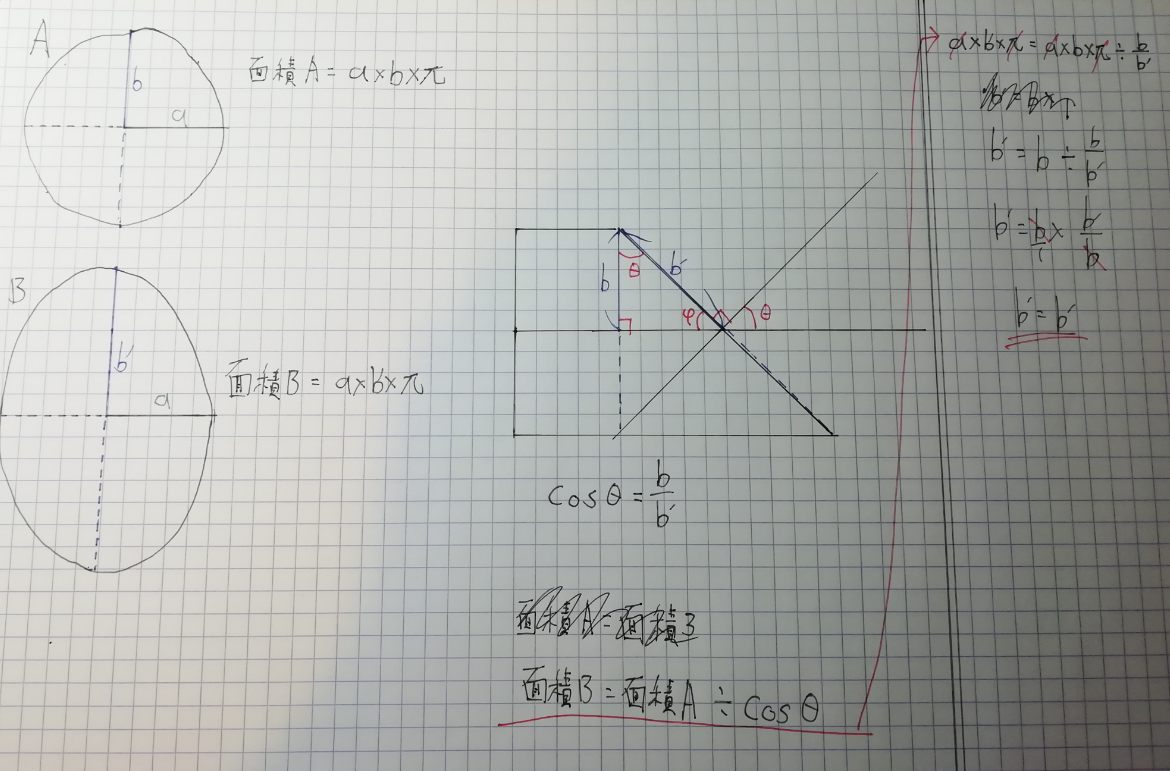
折角なので解説してみる。
まず正円Aの面積を半径a×半径b×πと表現する。正円なのでaとbの長さは同じだが、楕円に応用できるようにあえて記号を分けている。
次に楕円Bの面積を半径a×半径b'×πと表現する。
正円Aは棒を垂直に切った断面、楕円Bは同じ棒を角度をつけて切った断面である。
棒の断面を真横から見た図に、角度θ、正円の半径b、楕円の半径b'を記入する。
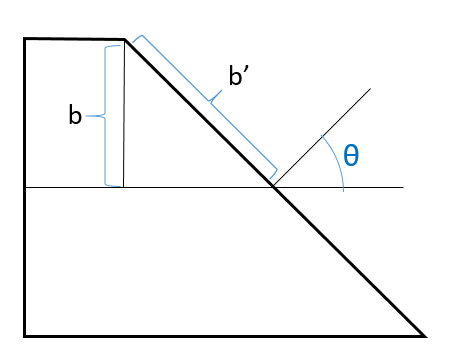
次に下図の青いθと赤いθが同じ角度であることを確認する。
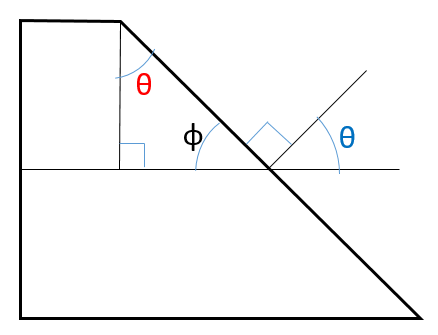
青θ+直角+φが180°であることが見て取れるが、三角形の内角の和も180°なのでφと直角を引くと当然θになる。よって青θと赤θは同一角である。
この三角形を取り出す。φは赤青θが同一であることを求めるための中間材料なのでこの後はもう使わない。
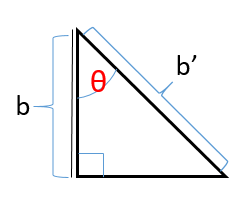
すると、cosθはbとb'の辺の比を表していることがわかる。
つまりcosθはb/b' である。
今分からないと言っている件は、面積B = 面積A / cosθであるということなので、この式に実際の辺の記号を割り当てて成り立つかどうかを確認していく。
↓
↓
↓
↓
↓
ということで成り立ってる。
以上、解説おわり。
終わりに
今回の問題が複雑かどうかは、それを考える人の数学レベルによると思う。私は数学が苦手な方なのでかなり難しく感じた。たった1行書かれていることを理解するのに4~5時間かかった。非常に疲れた。
しかし解決に至るまでの、なぜ分からないのか・どこで躓いているのかを自問しながら原因を探るプロセスは他の様々な問題解決に役立つとても良い経験になったような気がする。